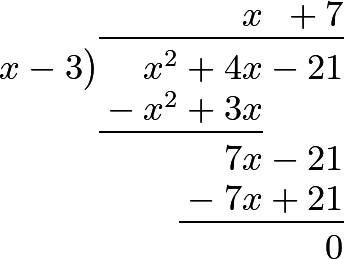Chapter 9. "Of the Nature of Equations of the Second Degree."
Part I. Section IV. Chapter 9. “Of the Nature of Equations of the Second Degree.”
689 What we have already said sufficiently shows, that equations of the second degree admit of two solutions; and this property ought to be examined in every point of view, because the nature of equations of a higher degree will be very much illustrated by such an examination. We shall therefore retrace, with more attention, the reasons which render an equation of the second degree capable of a double solution; since they undoubtedly will exhibit an essential property of those equations.
690 We have already seen, indeed, that this double solution arises from the circumstance that the square root of any number may be taken either positively, or negatively; but, as this principle will not easily apply to equations of higher degrees, it may be proper to illustrate it by a distinct analysis. Taking, therefore, for an example, the quadratic equation, \(x^2= 12x-35\), we shall give a new reason for this equation being resolvible in two ways, by admitting for \(x\) the values 5 and 7, both of which will satisfy the terms of the equation.
691 For this purpose it is most convenient to begin with transposing the terms of the equation, so that one of the sides may become 0; the above equation consequently takes the form \(x^2-12x+35=0\); and it is now required to find a number such, that, if we substitute it for \(x\), the quantity \(x^2 -12x + 35\) may be really equal to nothing; after which, we shall have to show how this may be done in two different ways.
692 Now, the whole of this consists in clearly showing, that a quantity of the form \(x^2 -12x + 35\) may be considered as the product of two factors. Thus, in reality, the quantity of which we speak is composed of the two factors \((x - 5) \cdot (x - 7)\); and since the above quantity must become 0, we must also have the product \((x-5) \cdot (x-7) = 0\); but a product, of whatever number of factors it is composed, becomes equal to 0, only when one of those factors is reduced to 0. This is a fundamental principle, to which we must pay particular attention, especially when equations of higher degrees are treated of.
693 It is therefore easily understood, that the product \((x - 5) \cdot (x - 7)\) may become 0 in two ways: first, when the first factor \(x-5 = 0\); and also, when the second factor \(x-7=0\). In the first case, \(x=5\), in the second \(x=7\). The reason is therefore very evident, why such an equation \(x^2-12x+35=0\), admits of two solutions; that is to say, why we can assign two values of \(x\), both of which equally satisfy the terms of the equation; for it depends upon this fundamental principle, that the quantity \(x^2 -12x + 35\) may be represented by the product of two factors.
694 The same circumstances are found in all equations of the second degree: for, after having brought the terms to one side, we find an equation of the following form \(x^2 -ax+ b=0\), and this formula may be always considered as the product of two factors, which we shall represent by \((x-p)(x-q)\), without considering what numbers the letters \(p\) and \(q\) represent, or whether they be negative or positive. Now, this product must be \(= 0\), from the nature of our equation, it is evident that this may happen in two cases; in the first place, when \(x= p\); and in the second place, when \(x=q\); and these are the two values of \(x\) which satisfy the terms of the equation,
695 Let us here consider the nature of these two factors, in order that the multiplication of the one by the other may exactly produce \(x^2 -ax+ b\). By actually multiplying them, we obtain \(x^2 -( p + q)x + pq\); which quantity must be the same as \(x^2 -ax+ b\), therefore we have evidently \(p+q=a\), and \(pq=b\). Hence is deduced this very remarkable property; that in every equation of the form \(x^2 -ax + b=0\), the two values of \(x\) are such, that their sum is equal to \(a\), and their product equal to \(b\): it therefore necessarilv follows, that, if we know one of the values, the other is easily found.
696 We have at present considered the case, in which the two values of \(x\) are positive, and which requires the second term of the equation to have the sign -, and the third term to have the sign +. Let us also consider the cases, in which either one or both values of \(x\) become negative. The first takes place, when the two factors of the equation give a product of this form, \((x-p) (x+q)\); for then the two values of \(x\) are \(x = p\), and \(x = - q\); and the equation itself becomes \(x^2 +(q-p)x-pq=0\); the second term having the sign + when \(q\) is greater than \(p\), and the sign - when \(q\) is less than \(p\); lastly, the third term is always negative.
The second case, in which both values of \(x\) are negative, occurs when the two factors are \((x+p) (x+q)\); for we shall then have \(x= -p\), and \(x= -q\); the equation itself therefore becomes \(x^2+(p +q)x+pq=0\). in which both the second and third terms are affected by the sign +.
697 The signs of the second and the third terms consequently show us the nature of the roots of any equation of the second degree. For let the equation be \(x^2 \dots ax \dots b=0\). If the second and third terms have the sign +, the two values of \(x\) are both negative; if the second term have the sign -, and the third term +, both values are positive: lastly, if the third term also have the sign -, one of the values in question is positive. But, in all cases whatever, the second term contains the sum of the two values, and the third term contains their product.
698 After what has been said, it will be easy to form equations of the second degree containing any two given values. Let there be required, for example, an equation such, that one of the values of \(x\) may be 7, and the other -3. We first form the simple equations \(x=7\), and \(x= -3\); whence, \(x-7=0\), and \(x+3=0\); these give us the factors of the equation required, which consequently becomes \(x^2 -4x-21 =0\). Applying here, also, the above rule, we find the two given values of \(x\); for if \(x^2=4x+21\), we have, by completing the square, etc. \(x=2 \pm \surd 25 =2 \pm 5\); that is to say, \(x=7\), or \(x= -3\).
699 The values of \(x\) may also happen to be equal. Suppose, for example, that an equation is required, in which both values may be 5. Here the two factors will be \((x-5) (x-5)\), and the equation sought will be \(x^2 - 10x + 25=0\). In this equation, \(x\) appears to have only one value; but it is because \(x\) is twice found \(= 5\), as the common method of resolution shows; for we have \(x^2= 10x-25\); wherefore \(x=5\pm \surd 0 = 5 \pm 0\), that is to say, \(x\) is in two ways \(= 5\).
700 A very remarkable case sometimes occurs, in which both values of \(x\) become imaginary, or impossible; and it is then wholly impossible to assign any value for \(x\), that would satisfy the terms of the equation. Let it be proposed, for example, to divide the number 10 into two parts, such that their product may be 30. If we call one of those parts \(x\), the other will be \(10-x\), and their product will be \(10x-x^2=30\); wherefore \(x^2= 10x-30\), and \(x=5 \pm \surd -5\), which, being an imaginary number, shows that the question is impossible.
701 It is very important, therefore, to discover some sign, by means of which we may immediately know whether an equation of the second degree be possible or not.
Let us resume the general equation \(x^2 -ax+b=0\). We shall have \(x^2=ax - b\), and \(x =\frac{1}{2}a \pm \surd\left(\frac{1}{4}a^2-b\right)\). This shows, that if \(b\) be greater than \(\frac{1}{4}a^2\), or \(4b\) greater than \(a^2\), the two values of \(x\) are always imaginary, since it would be required to extract the square root of a negative quantity; on the contrary, if \(b\) be less than \(\frac{1}{4}a^2\), or even less than 0, that is to say, if it be a negative number, both values will be possible or real. But, whether they be real or imaginary, it is no less true, that they are still expressible, and always have this property, that their sum is equal to \(a\), and their product equal to \(b\). Thus, in the equation \(x^2 -6x+ 10=0\), the sum of the two values of \(x\) must be 6, and the product of these two values must be 10; now, we find,
\[\textrm{I)} \; x= 3 + \surd -1,\]and
\[\textrm{II)} \; x=3-\surd -1,\]quantities whose sum is 6, and the product 10.
702 The expression which we have just found may likewise be represented in a manner more general, and so as to be applied to equations of this form, \(fx^2 \pm gx + h=0\); for this equation gives
\[x^2=\mp \dfrac{gx}{f} - \dfrac{h}{f},\]and
\[x= \mp \dfrac{g}{2f} \pm \surd \left(\frac{g^2}{4f^2}-\frac{h}{f}\right),\]or
\[x = \dfrac{\mp g \pm \surd(g^2-4fh)}{2f};\]whence we conclude, that the two values are imaginary, and consequently, the equation impossible, when \(4fh\) is greater than \(g^2\); that is to say, when, in the equation \(fx^2 - gx + h=0\), four times the product of the first and the last term exceeds the square of the second term: for the product of the first and the last term, taken four times, is \(4fhx^2\), and the square of the middle term is \(g^2x^2\); now, if \(4fhx^2\) be greater than \(g^2x^2\), \(4fh\) is also greater than \(g^2\), and, in that case, the equation is evidently impossible; but in all other cases, the equation is possible, and two real values of \(x\) may be assigned. It is true, they are often irrational; but we have already seen, that, in such cases, we may always find them by approximation: whereas no approximations can take place with regard to imaginary expressions, such as \(\surd -5\); for 100 is as far from being the value of that root, as 1, or any other number.
703 We have farther to observe, that any quantity of the second degree, \(x^2 \pm ax \pm b\), must always be resolvible into two factors, such as
\[(x \pm p) (x \pm q).\]For, if we took three factors, such as these, we should come to a quantity of the third degree; and taking only one such factor, we should not exceed the first degree. It is therefore certain, that every equation of the second degree necessarily contains two values of \(x\), and that it can neither have more nor less
704 We have already seen, that when the two factors are found, the two values of \(x\) are also known, since each factor gives one of those values, by making it equal to 0. The converse also is true, viz. that when we have found one value of \(x\), we know also one of the factors of the equation; for if \(x=p\) represents one of the values of \(x\), in any equation of the second degree, \(x-p\) is one of the factors of that equation; that is to say, all the terms having heen brought to one side, the equation is divisible by \(x - p\); and farther, the quotient expresses the other factor.
705 In order to illustrate what we have now said, let there be given the equation \(x^2+4x-21=0\), in which we know that \(x=3\) is one of the values of \(x\), because \((3 \cdot 3)+(4 \cdot 3)-21=0\); this shows, that \(x-3\) is one of the factors of the equation, or that \(x^2+4x-21\) is divisible by \(x-3\), which the actual division proves. Thus,
So that the other factor is \(x + 7\), and our equation is represented by the product \((x-3) (x+7)=0\); whence two values of \(x\) immediately follow, the first factor giving \(x=3\), and the other \(x= -7\).
Editions
- Leonhard Euler. Elements of Algebra. Translated by Rev. John Hewlett. Third Edition. Longmans, Hurst, Rees, Orme, and Co. London. 1822.
- Leonhard Euler. Vollständige Anleitung zur Algebra. Mit den Zusätzen von Joseph Louis Lagrange. Herausgegeben von Heinrich Weber. B. G. Teubner. Leipzig and Berlin. 1911. Leonhardi Euleri Opera omnia. Series prima. Opera mathematica. Volumen primum.